本文旨在阐述启动DSA(数据结构与算法)所需的基本知识单元。
许多前端开发者,包括我自己,常常质疑学习dsa的必要性,因为日常开发中并不总是需要它。然而,在某些情况下,dsa至关重要,例如当需要优化性能以避免用户关闭缓慢加载的网页选项卡时。 理解时间复杂度和高效算法有助于编写更优化的代码,从而提升可扩展性。
本文将涵盖以下内容:
- 数据结构是什么?
- 时间复杂度是什么?
- 空间复杂度是什么?
- 如何简化复杂度分析?
让我们开始吧!
什么是数据结构? 数据结构可由三个要素定义:
- 一个数据集;
- 数据项之间的关系或链接;
- 可对数据执行的操作或函数。
例如,数组 arr = [12, 54, 86, 3, 94] 满足以上三个条件:
- 收集数据 (✔️)
- 关系或链接:每个数组元素都有唯一的索引 (✔️)
- 可执行操作:例如,
arr.push(7)(✔️)
因此,数组是一种有效的数据结构。
什么是时间复杂度? 时间复杂度描述的是算法执行时间与输入规模之间的关系。
需要注意的是,时间复杂度并非以秒为单位衡量实际执行时间,而是通过操作数量来衡量。这是因为不同硬件的执行速度不同,但对于相同的输入,算法的操作数量保持不变。
让我们通过一个例子来理解:求n个数字的和。 有两种方法:
方法一:使用公式 (n * (n - 1)) / 2
方法二:累加 sum = (n - 1) + (n - 2) + ... + 1
方法一:
旅游网站管理系统是由深山工作室自主研发而成,具有以下相应的功能.1. 旅游新闻发布,站内新闻发布2. 发布旅游线路详细信息.包括:线路名称、线路类型、线路报价、游完整条线路所需时间、线路说明、线路途经景点、行程安排及其它备注。3. 旅游景点介绍推广4. 旅行社加盟介绍系统.包括:各个旅行社可以发布自己的旅游线路.管理留言,发布信息(vip,会员)5. 酒店宾馆加盟介绍系统,酒店宾馆发布客房信息(v
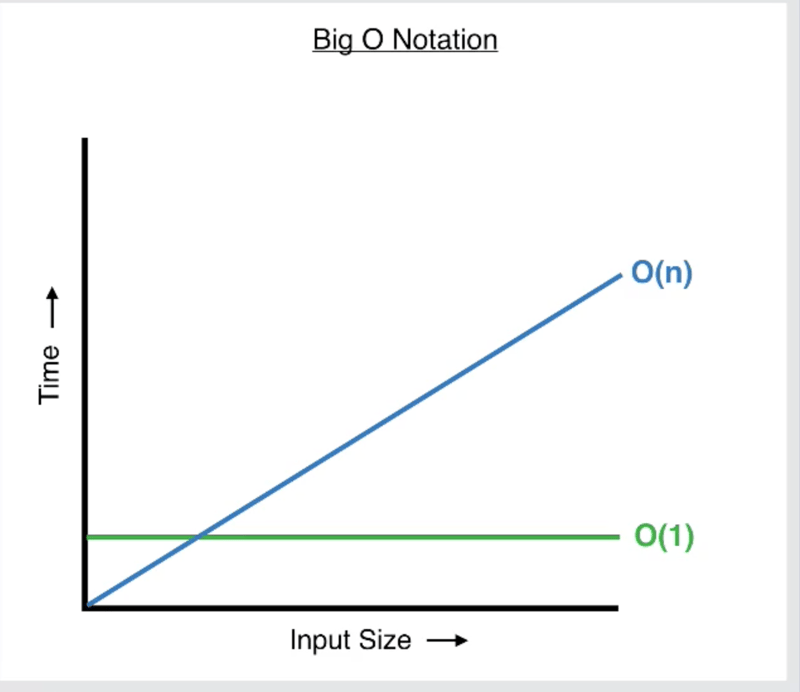
- 操作数量恒定为3,与n无关。时间复杂度为O(1) (常数时间)。
方法二:
- 操作数量为2n - 3。随着n的增加,操作数量线性增加。时间复杂度为O(n) (线性时间)。
我们使用大O符号表示时间复杂度。
一些常见的时间复杂度:
- O(1):常数时间
- O(n):线性时间
- O(log n):对数时间 (例如,二进制搜索)
- O(n log n):线性对数时间 (例如,归并排序)
- O(n²), O(n³), ...:多项式时间 (例如,嵌套循环)
- O(2ⁿ):指数时间 (例如,斐波那契数列)
- O(n!):阶乘时间
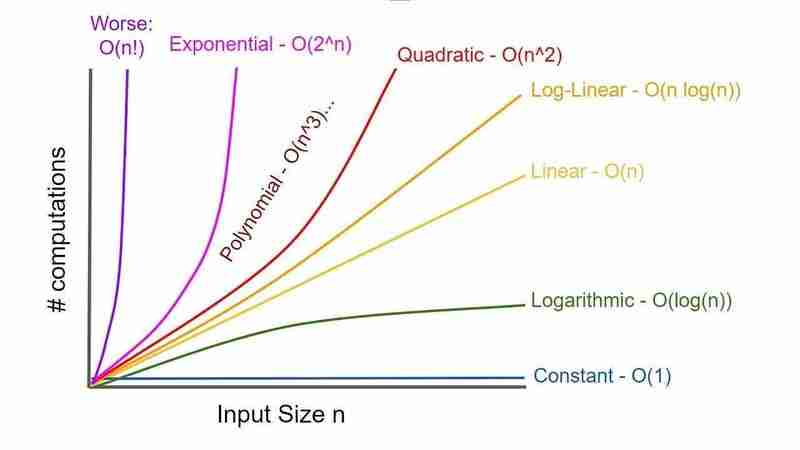
简化复杂度分析 (大O):
- 忽略常数:例如,O(7n²) 简化为 O(n²)
- 忽略低阶项:例如,O(n³ + n²) 简化为 O(n³)
- 不要忽略其他输入变量:例如,O(n³m²) 不能简化为 O(n³)
基于以上,方法二的时间复杂度简化为O(n)。
什么是空间复杂度? 空间复杂度描述的是算法所需的辅助空间与输入规模之间的关系。 我们只考虑算法额外使用的空间,而不考虑输入本身占用的空间。 同样使用大O符号表示。
例如,如果算法使用的辅助空间与输入规模无关,则空间复杂度为O(1)。
思考题:
为什么O(1)比O(n)更好?





























