当我们有一个
先序遍历序列:1,3,7,9,5,11
中序遍历序列:9,7,3,1,5,11
我们可以很轻松的用笔写出对应的二叉树。但是用代码又该如何实现?
下面我们来简单谈谈基本思想。
首先,先序遍历的顺序是根据 根-左孩子-右孩子 的顺序遍历的,那么我们可以率先确认的是先序遍历序列的第一个数就是根节点,然后中序遍历是根据 左孩子-根-右孩子 的顺序遍历的。我们通过先序遍历确认了根节点,那么我们只需要在中序遍历中找到根节点的位置,然后就可以很好地区分出,那些属于左子树的节点,那些是属于右子树的节点了。如下图:
我们确定数字1为根节点,然后根据中序遍历的遍历顺序确定,中序遍历序列中数字1的左边全部为左子树节点,右边全部为右子树。通过左子树节点的个数,得出先序遍历序列中从根节点往后的连续3个数是属于左子树的,剩下的为右子树。这样再在左右子树的序列中重复以上步骤,最终找到没有子节点为止。

实现代码如下:
1 package com.tree.traverse; 2 3 import java.util.ArrayList; 4 import java.util.List; 5 6 /** 7 * @author Caijh 8 * 9 * 2017年6月2日 下午7:21:10 10 */ 11 12 public class BuildTreePreOrderInOrder { 13 14 /** 15 * 1
16 * / \ 17 * 3 5
18 * / \ 19 * 7 11 20 * /
21 * 9
22 */ 23 public static int treeNode = 0;//记录先序遍历节点的个数 24 private List nodeList = new ArrayList<>();//层次遍历节点的队列 25 public static void main(String[] args) { 26 BuildTreePreOrderInOrder build = new BuildTreePreOrderInOrder(); 27 int[] preOrder = { 1, 3, 7, 9, 5, 11}; 28 int[] inOrder = { 9, 7, 3, 1, 5, 11}; 29 30 treeNode = preOrder.length;//初始化二叉树的节点数 31 Node root = build.buildTreePreOrderInOrder(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1); 32 System.out.print("先序遍历:"); 33 build.preOrder(root); 34 System.out.print("\n中序遍历:"); 35 build.inOrder(root); 36 System.out.print("\n原二叉树:\n"); 37 build.prototypeTree(root); 38 } 39 40 /** 41 * 分治法 42 * 通过先序遍历结果和中序遍历结果还原二叉树 43 * @param preOrder 先序遍历结果序列 44 * @param preOrderBegin 先序遍历起始位置下标 45 * @param preOrderEnd 先序遍历末尾位置下标 46 * @param inOrder 中序遍历结果序列 47 * @param inOrderBegin 中序遍历起始位置下标 48 * @param inOrderEnd 中序遍历末尾位置下标 49 * @return 50 */ 51 public Node buildTreePreOrderInOrder(int[] preOrder, int preOrderBegin, int preOrderEnd, int[] inOrder, int inOrderBegin, int inOrderEnd) { 52 if (preOrderBegin > preOrderEnd || inOrderBegin > inOrderEnd) { 53 return null; 54 } 55 int rootData = preOrder[preOrderBegin];//先序遍历的第一个字符为当前序列根节点 56 Node head = new Node(rootData); 57 int divider = findIndexInArray(inOrder, rootData, inOrderBegin, inOrderEnd);//找打中序遍历结果集中根节点的位置 58 int offSet = divider - inOrderBegin - 1;//计算左子树共有几个节点,节点数减一,为数组偏移量 59 Node left = buildTreePreOrderInOrder(preOrder, preOrderBegin + 1, preOrderBegin + 1 + offSet, inOrder, inOrderBegin,inOrderBegin + offSet); 60 Node right = buildTreePreOrderInOrder(preOrder, preOrderBegin + offSet + 2, preOrderEnd, inOrder, divider + 1, inOrderEnd); 61 head.left = left; 62 head.right = right; 63 return head; 64 } 65 /** 66 * 通过先序遍历找到的rootData根节点,在中序遍历结果中区分出:中左子树和右子树 67 * @param inOrder 中序遍历的结果数组 68 * @param rootData 根节点位置 69 * @param begin 中序遍历结果数组起始位置下标 70 * @param end 中序遍历结果数组末尾位置下标 71 * @return return中序遍历结果数组中根节点的位置 72 */ 73 public int findIndexInArray(int[] inOrder, int rootData, int begin, int end) { 74 for (int i = begin; i <= end; i++) { 75 if (inOrder[i] == rootData) 76 return i; 77 } 78 return -1; 79 } 80 /** 81 * 二叉树先序遍历结果 82 * @param n 83 */ 84 public void preOrder(Node n) { 85 if (n != null) { 86 System.out.print(n.val + ","); 87 preOrder(n.left); 88 preOrder(n.right); 89 } 90 } 91 /** 92 * 二叉树中序遍历结果 93 * @param n 94 */ 95 public void inOrder(Node n) { 96 if (n != null) { 97 inOrder(n.left); 98 System.out.print(n.val + ","); 99 inOrder(n.right);100 }101 }102 /**103 * 还原后的二叉树104 * 二叉数层次遍历105 * 基本思想:106 * 1.因为推导出来的二叉树是保存在Node类对象的子对象里面的,(类似于c语言的结构体)如果通过递归实现层次遍历的话,不容易实现107 * 2.这里采用List队列逐层保存Node对象节点的方式实现对二叉树的层次遍历输出108 * 3.如果父节点的位置为i,那么子节点的位置为,2i 和 2i+1;依据这个规律逐层遍历,通过保存的父节点,找到子节点。并保存,不断向下遍历保存。109 * @param tree110 */111 public void prototypeTree(Node tree){112 //用list存储层次遍历的节点113 if(tree !=null){114 if(tree!=null)115 nodeList.add(tree);116 nodeList.add(tree.left);117 nodeList.add(tree.right);118 int count=3;119 //从第三层开始120 for(int i=3;count=treeNode)//当所有有效节点都遍历到了就结束遍历137 break;138 j+=2;//每次存储两个子节点,所以每次加2139 }140 }141 int flag=0,floor=1;142 for(Node node:nodeList){143 if(node!=null)144 System.out.print(node.val+" ");145 else146 System.out.print("# ");//#号表示空节点147 flag++;148 /**149 * 逐层遍历输出二叉树150 *
151 */152 if(flag>=Math.pow(2, floor-1)){153 flag=0;154 floor++;155 System.out.println();156 }157 }158 }159 }160 /**161 * 内部类162 * 1.每个Node类对象为一个节点,163 * 2.每个节点包含根节点,左子节点和右子节点164 */165 class Node {166 Node left;167 Node right;168 int val;169 public Node(int val) {170 this.val = val;171 }172 }173 }
运行结果:
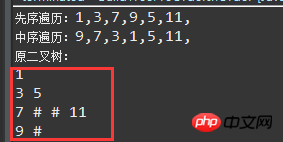
最后逐层输出二叉树的基本思想:
* 1.因为推导出来的二叉树是保存在Node类对象的子对象里面的,(类似于c语言的结构体)如果通过递归实现层次遍历的话,不容易实现
* 2.这里采用List队列逐层保存Node对象节点的方式实现对二叉树的层次遍历输出
* 3.如果父节点的位置为i,那么子节点的位置为,2i 和 2i+1;依据这个规律逐层遍历,通过保存的父节点,找到子节点。并保存,不断向下遍历保存。































