给定一个正整数 n,并构造一个 n x n 的螺旋矩阵,仅在顺时针方向上使用 o(1) 额外空间
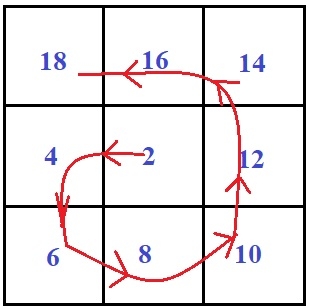
螺旋矩阵是一个像螺旋一样工作的矩阵,它将开始从圆的原点开始,按顺时针方向旋转。因此,任务是使用从 2 → 4 → 6 → 8 → 10 → 12 → 14 → 1 6→ 18 开始的 O(1) 空间以螺旋形式打印矩阵。
下面是示例螺旋矩阵 -
示例
Input: 3 Output: 9 8 7 2 1 6 3 4 1
解决具有无限空间的代码变得很容易,但这并不像最佳程序那样有效,或者代码在内存和时间上都是有效的。因此,为了保持螺旋顺序,使用了四个循环,每个循环用于矩阵的上、右、下和左角,但是如果我们将矩阵分为两部分,即右上角和左下角,我们可以直接使用这个概念
mat[i][j] = (n-2*x)*(n-2*x)-(i-x)-(j-x)
对于左下半部分,
mat[i][j] = (n-2*x-2)*(n-2*x-2) + (i-x) + (j-x)
注意-我们正在编写用于打印 2 的矩阵倍数的程序
算法
int spiralmatrix(int n)
START
STEP 1: DECLARE i, j, a, b, x
STEP 2: LOOP FOR i = 0 AND i < n AND i++
LOOP FOR j = 0 AND j < n AND j++
FIND THE MINIMUM IN (i示例
#include
//For n x n spiral matrix
int spiralmatrix(int n){
int i, j, a, b, x; // x stores the layer in which (i, j)th element exist
for ( i = 0; i < n; i++){
for ( j = 0; j < n; j++){
// Finds minimum of four inputs
a = ((i");
}
}
int main(int argc, char const *argv[]){
int n = 3;
spiralmatrix(n);
return 0;
}
输出
如果我们运行上面的程序,那么它将生成以下输出 -
18 16 14
4 2 12
6 8 10




























