简介
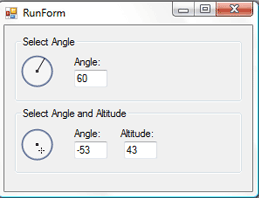
Adobe Photoshop有两个非常专业的用来设置如投影、斜面与浮雕等特效的控件：一个是角度选择器，另一个是角度与高度选择器（如上图所示）。
本文将带领读者创建两个自定义控件，来模仿Photoshop中这两个控件的外观和行为。
基础知识——数学
毕达哥拉斯定理
（即勾股定理，为尊重原文，以下简称毕氏定理。尽管有点绕口。——野比注）
利用毕氏定理，我们可以计算直角三角形的斜边（最长边）。计算公式为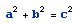
。这样，斜边c就等于
。
单位圆
鉴于接下来的工作和角度及圆有关，我们先熟悉一下单位圆的形式是很有好处的。单位圆就是以(0,0)为圆心，半径为1的圆。在常规网格（指画布——野比注）中，0度（的坐标）从(1,0)这点（右）开始，按逆时针方向增大。因此，90度是(0,1)，180度是(-1,0)，270度是(0,-1)，最后360度和0点重合。
三角函数
这里我们只需要知道三个基本的三角函数：sin、cos和tan（正弦、余弦和正切——野比注）。如果我们还记得SOH-CAH-TOA（译注+）的话，我们就知道，（直角）三角形的正弦等于对边比上斜边，余弦等于邻边比上斜边，正切等于对边比上邻边。
同样，我们知道反三角函数用来计算未知角度。
译注+：
SOH-CAH-TOA是老外用来记忆三角函数的口诀。其中：O为opposite（对边），H为Hypotenuse（斜边），A为Adjacent（邻边）。
SOH: Sine = Opposite ÷ Hypotenuse
CAH: Cosine = Adjacent ÷ Hypotenuse
TOA: Tangent = Opposite ÷ Adjacent
常用函数
我们制作的自定义控件都会用到下面这两个重要的函数（方法）：
一个函数接收角度和半径作为参数，返回围绕某个原点的相应点位置。（简单来说，就是把角度转换为点）
一个完成相反的功能，以点(X, Y)作为参数，找到最匹配的角度。
第一个函数要简单些：
private PointF DegreesToXY(float degrees, float radius, Point origin)
{
PointF xy = new PointF();
double radians = degrees * Math.PI / 180.0;
xy.X = (float)Math.Cos(radians) * radius + origin.X;
xy.Y = (float)Math.Sin(-radians) * radius + origin.Y;
return xy;
}要注意的是首先我们需要把角度换算成弧度。一般来说，我们只需要在单位圆中进行研究：
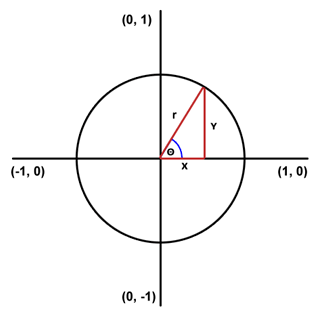
该函数已知角度和半径，利用三角函数，我们算出X和Y值，然后在加上给定的原点初始坐标即可。
还应看到，函数代码中用到的是Y分量的负值，这是因为计算机显示器上网格是上下颠倒的（向下为正）。
第二个函数的功能是把用户在控件上点击的点位置转换为相应的角度值。这稍稍麻烦点，因为我们不得不考虑添加一些东西。限于文章篇幅，我这里贴出部分代码：
private float XYToDegrees(Point xy, Point origin)
{
double angle = 0.0;
if (xy.Y < origin.Y)
{
if (xy.X > origin.X)
{
angle = (double)(xy.X - origin.X) / (double)(origin.Y - xy.Y);
angle = Math.Atan(angle);
angle = 90.0 - angle * 180.0 / Math.PI;
}
else if (xy.X < origin.X)
{
//如此这般
}
}
else if (xy.Y > origin.Y)
{
//如此这般
}
if (angle > 180) angle -= 360; //控制角度范围
return (float)angle;
}该函数主要通过检查鼠标相对中心点的位置，确定其所在象限。一旦我们知道了象限，就可以利用三角函数（反正切）计算出角度。
如果角度大于180度，则减去360度。这样就和Photoshop一样，把角度控制在-180度和180度之间。当然，这一步可以不做，不加这行代码控件一样能用。
制作控件
绘制控件
这两个控件的背景相同：
用宽度为2的Pen绘制外圈圆
用40%（约100）不透明度的白色填充
控件中心是3x3像素的正方形
protected override void OnPaint(PaintEventArgs e)
{
//...
//Draw
g.SmoothingMode = SmoothingMode.AntiAlias;
g.DrawEllipse(outline, drawRegion);
g.FillEllipse(fill, drawRegion);
//...光标
g.SmoothingMode = SmoothingMode.HighSpeed;
g.FillRectangle(Brushes.Black, originSquare);
//...
}注意SmoothMode属性。在绘制圆圈时将该属性设置为AntiAlias（抗锯齿），这样看起来既光滑又专业。但是如果画正方形时也用抗锯齿，就会显得模糊难看，所以将SmoothMode设置为HighSpeed（高速），这样画出的正方形边缘整齐犀利。
根据控件不同，光标也有不同绘制方法。角度选择器比较简单，只需要从圆心到DegreesToXY函数返回的点连一条直线即可。角度与高度选择器则是在这点上绘制一个1x1的矩形，然后在周围绘制一个十字型光标。
处理用户点击
多亏我们有了XYToDegrees函数，处理用户点击变得特别简单。为了让我们的控件用起来和Photoshop一模一样，我们需要设置MouseDown和MouseMove事件。这样，各项数值将实时更新。这里是一个附注函数的代码：
private int findNearestAngle(Point mouseXY)
{
int thisAngle = (int)XYToDegrees(mouseXY, origin);
if (thisAngle != 0)
return thisAngle;
else
return -1;
}高度控件需要额外的处理，就是找到中心点和鼠标点击点的距离：
private int findAltitude(Point mouseXY)
{
float distance = getDistance(mouseXY, origin);
int alt = 90 - (int)(90.0f * (distance / origin.X));
if (alt < 0) alt = 0;
return alt;
}在Photoshop中，选择点（指鼠标点击点）在圆心时，高度为90，在边缘处则为0。这样，我们可以通过找到点击点到圆心距离和半径高度比值来计算出高度。然后，用90减去该值（实际上是按90到0来翻转一下）。
自定义事件
为了让我们的自定义控件更加专业，需要控件能够在数值发生变化时以编程方式进行提醒。这就是我们要设置事件的原因。
例如，像这样给角度变化添加一个事件：
public delegate void AngleChangedDelegate(); public event AngleChangedDelegate AngleChanged;
然后，我们要做的就是每次变更Angle属性时，调用AngleChanged()（需要先判断是否为null）。
限制与改进
闪烁
没有闪烁！只需要在制作控件时设置DoubleBuffered属性为true，.NET Framework 2.0会处理剩下的工作，保证控件能流畅的重绘。
尺寸
因为控件使用基于半径（圆）的数学计算方法，因此需要保证控件的长度和宽度相等。
颜色
我是照着Photoshop的样子来的，所以并没包含背景颜色、外圈颜色这些属性。但是，浏览下代码，你会发现改成你喜欢的颜色或者让颜色可以动态修改并不是什么难事。
结论
我建议你下载项目文件（或者至少下载DEMO），这样你可以看到这俩控件用起来很爽。
协议
本文及有关代码、程序均基于CPOL（Codeproject Open License）协议。
更多Photoshop样式的角度和高度选择器控件 相关文章请关注PHP中文网！
