深度学习能够取得如此成就,得益于其能够相对轻松地解决大规模非凸优化问题。尽管非凸优化是 NP 困难的,但一些简单的算法,通常是随机梯度下降(SGD)的变体,它们在实际拟合大型神经网络时表现出惊人的有效性。
本文中,来自华盛顿大学的多位学者撰文《 Git Re-Basin: Merging Models modulo Permutation Symmetries 》,他们研究了在深度学习中,SGD 算法在高维非凸优化问题上的不合理有效性。他们受到三个问题的启发:
1. 为什么 SGD 在高维非凸深度学习损失 landscapes 的优化中表现良好,而在其他非凸优化设置中,如 policy 学习、轨迹优化和推荐系统的稳健性明显下降 ?
2. 局部极小值在哪里?在初始化权值和最终训练权值之间进行线性插值时,为什么损失会平滑、单调地减小?
3. 两个独立训练的模型,它们具有不同的随机初始化和数据批处理顺序,为何会实现几乎相同的性能?此外,为什么它们的训练损失曲线看起来一样
☞☞☞AI 智能聊天, 问答助手, AI 智能搜索, 免费无限量使用 DeepSeek R1 模型☜☜☜

论文地址:https://arxiv.org/pdf/2209.04836.pdf
本文认为:在模型训练中存在一些不变性,这样一来才会有不同的训练表现出几乎相同的性能。
为什么会这样呢?2019 年,Brea 等人注意到神经网络中的隐藏单元具有排列对称性。简单的说就是:我们可以交换网络中隐藏层的任意两个单元,而网络功能将保持不变。2021 年 Entezari 等人推测,这些排列对称可能允许我们在权值空间中线性连接点,而不损害损失。
下面我们以论文作者之一的举例来说明文章主旨,这样大家会更清楚。
假如说你训练了一个 A 模型,你的朋友训练了一个 B 模型,这两个模型训练数据可能不同。没关系,使用本文提出的 Git Re-Basin,你能在权值空间合并这两个模型 A+B,而不会损害损失。
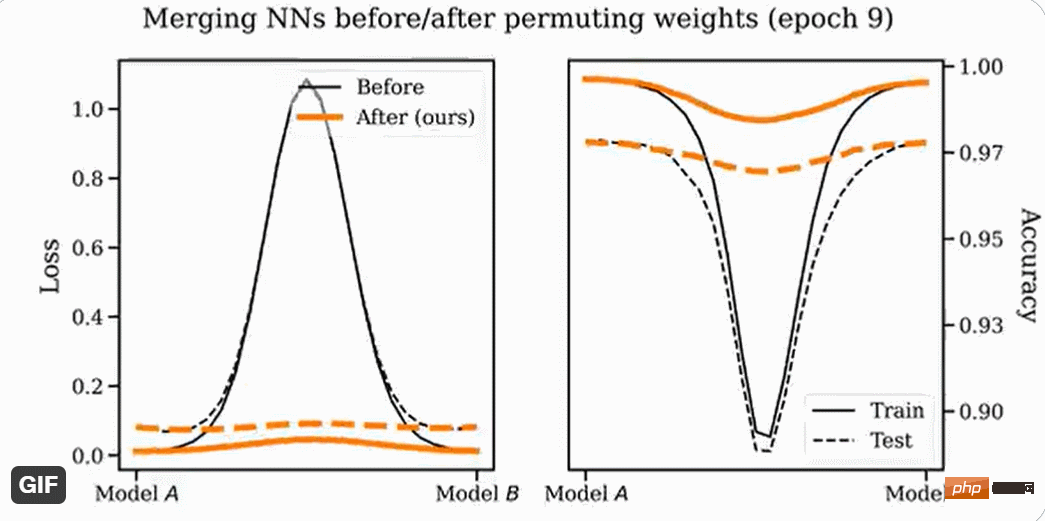
论文作者表示,Git Re-Basin 可适用于任何神经网络(NN),他们首次演示了在两个独立训练(没有预先训练)的模型(ResNets)之间,可以零障碍的线性连通。
他们发现,合并能力是 SGD 训练的一个属性,在初始化时合并是不能工作的,但是会发生相变,因此随着时间的推移合并将成为可能。
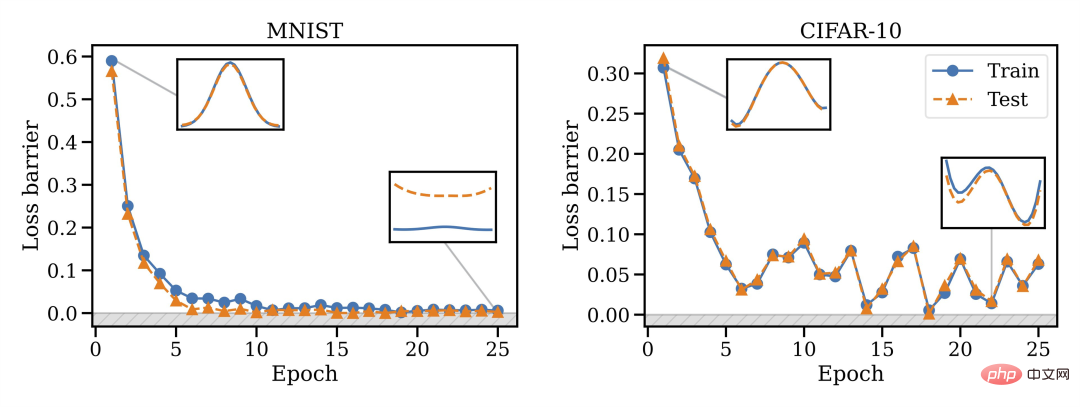
他们还发现,模型宽度与可合并性密切相关,即越宽越好。
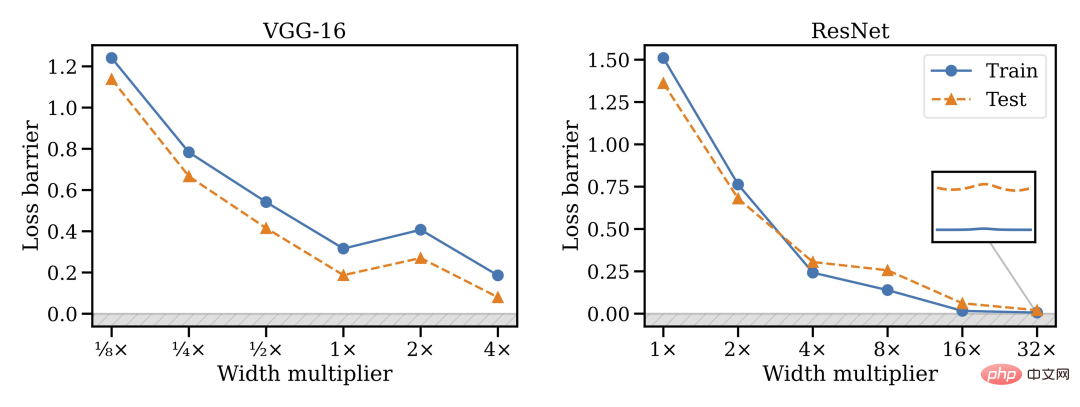
此外,并非所有架构都能合并:VGG 似乎比 ResNets 更难合并。
这种合并方法还有其他优点,你可以在不相交和有偏差的数据集上训练模型,然后在权值空间中将它们合并在一起。例如,你有一些数据在美国,一些在欧盟。由于某些原因,不能混合数据。你可以先训练单独的模型,然后合并权重,最后泛化到合并的数据集。
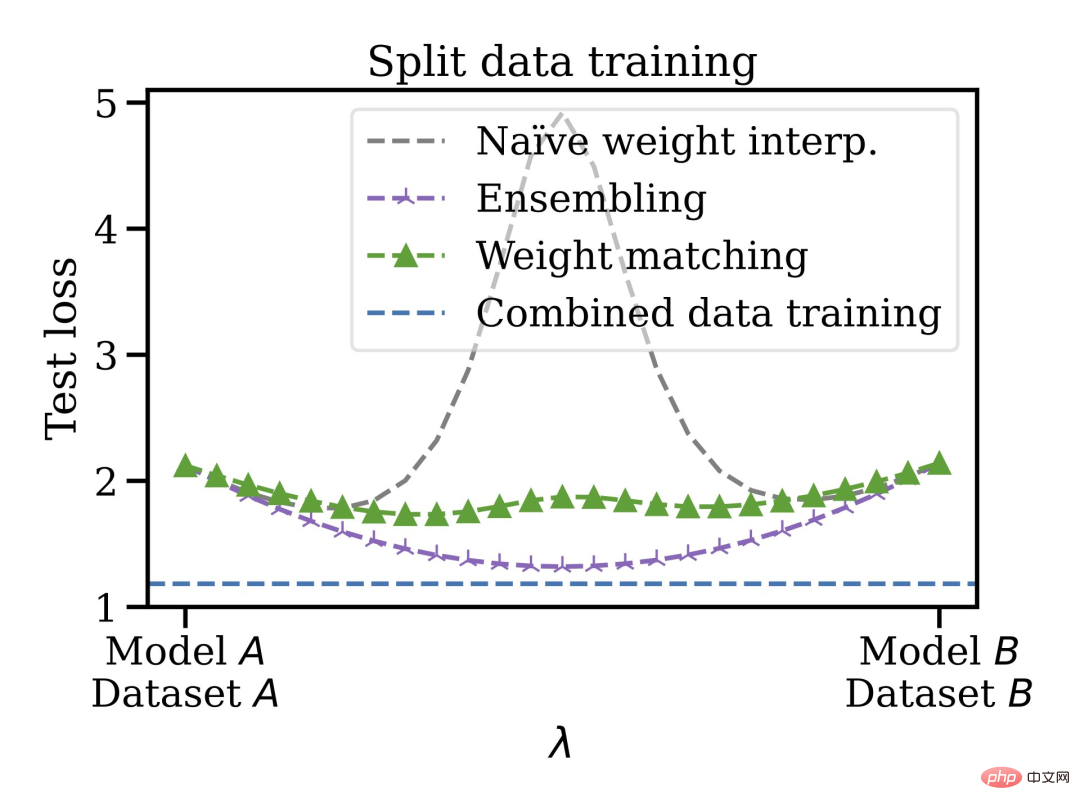
因此,在不需要预训练或微调的情况下可以混合训练过的模型。作者表示自己很想知道线性模式连接和模型修补的未来发展方向,可能会应用到联邦学习、分布式训练以及深度学习优化等领域。
最后还提到,章节 3.2 中的权重匹配算法只需 10 秒左右即可运行,所以节省了大量时间。论文第 3 章也介绍了 A 模型与 B 模型单元匹配的三种方法,对匹配算法还不清楚的小伙伴,可以查看原论文。
网友评论及作者解疑
这篇论文在推特上引发了热议,PyTorch 联合创始人 Soumith Chintala 表示如果这项研究可以迁移到更大的设置,则它可以实现的方向会更棒。合并两个模型(包括权重)可以扩展 ML 模型开发,并可能在开源的共同开发模型中发挥巨大作用。
另有人认为如果排列不变性能够这样高效地捕捉大部分等价性,它将为神经网络的理论研究提供启发。
论文一作、华盛顿大学博士 Samuel Ainsworth 也解答了网友提出的一些问题。
首先有人问,「论文中是否有关于在训练中针对独特 basin 的任何提示?如果有一种方法可以做到对排列进行抽象,那么训练速度可能会更快。」
Ainsworth 回复称,这点自己没有想到。他真的希望能够以某种方式实现更快地训练,但目前为止已被证明非常困难。问题在于 SGD 本质上是一种局部搜索,因此利用高阶几何并不是那么容易。也许分布式训练是一种可行的方法。
还有人问是否适用于 RNN 和 Transformers?Ainsworth 表示原则上适用,但他还没有对此进行实验。时间会证明一切。
最后有人提出,「这看起来对分布式训练『成真』非常重要?难道 DDPM(去噪扩散概率模型)不使用 ResNet 残差块吗?」
Ainsworth 回复称,虽然他自己对 DDPM 不是很熟悉,但直言不讳表示将它用于分布式训练将非常令人兴奋。