一个映射是满射当且仅当其值域等于目标集合,即对目标集中任意元素,原像集中都存在至少一个元素与之对应。通过选取任意目标元素、构建方程 $f(x) = y$、求解并验证解在原像集中,可证明满射;反例或值域分析则可证非满射。函数的形态、定义域与目标集匹配程度等均影响满射性。
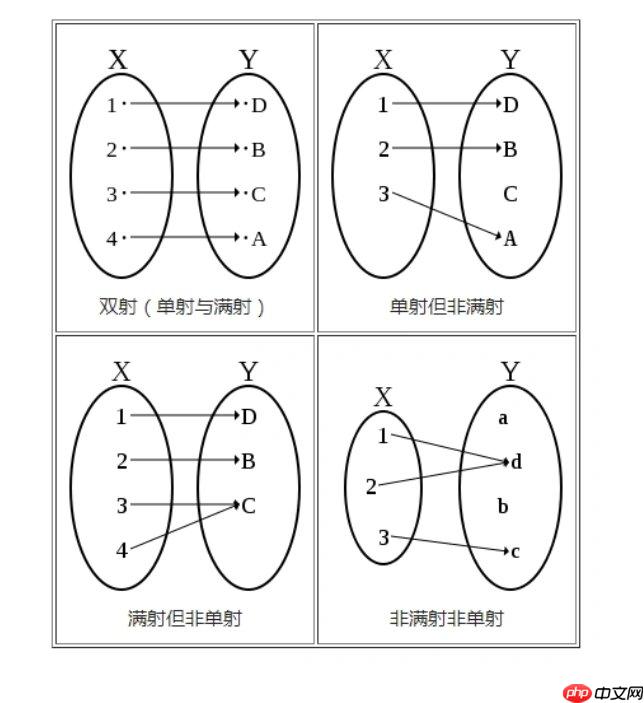
理解一个映射是否“满射”(Surjective,或称“映上”),核心在于它是否能“覆盖”到目标集合的每一个角落。简单来说,就是目标集合(Codomain)里的任何一个元素,都能在原像集合(Domain)中找到至少一个“源头”与之对应。我们证明满射,通常就是从目标集合里任意抓一个元素,然后想办法证明,总能从原像集合里找到一个输入,通过这个映射,正好能得到我们抓出来的那个元素。
解决方案
要证明一个映射 $f: A \to B$ 是满射,我们通常会遵循以下步骤,这其实是一个逆向工程的过程:
- 选取任意目标元素: 从目标集合 $B$ 中选取一个任意的元素,我们通常用 $y$ 来表示它。
- 构建方程: 设定方程 $f(x) = y$。我们的目标是找到一个 $x$(原像)使得这个等式成立。
- 求解 $x$: 尝试解出 $x$,用 $y$ 的表达式来表示 $x$。
- 验证 $x$ 的有效性: 最关键的一步!检查你解出来的 $x$ 是否确实属于原像集合 $A$。如果对于任何选定的 $y \in B$,你总能找到一个 $x \in A$ 使得 $f(x) = y$,那么这个映射就是满射。
让我们通过几个具体例子来感受一下这个过程。
例题 1:一个简单的线性函数
考虑映射 $f: \mathbb{R} \to \mathbb{R}$,定义为 $f(x) = 2x + 3$。
- 选取任意 $y \in \mathbb{R}$(目标集合 $\mathbb{R}$)。
- 构建方程: 设 $f(x) = y$,即 $2x + 3 = y$。
- 求解 $x$: $2x = y - 3$ $x = \frac{y - 3}{2}$
- 验证 $x$ 的有效性: 因为 $y$ 是任意实数,那么 $y - 3$ 也是实数,$\frac{y - 3}{2}$ 自然也是实数。这意味着,对于目标集合中的任何实数 $y$,我们总能找到一个实数 $x = \frac{y - 3}{2}$ 作为它的原像。而且,这个 $x$ 属于原像集合 $\mathbb{R}$。
因此,映射 $f(x) = 2x + 3$ 是满射。
例题 2:一个二次函数,但目标集合被限制
考虑映射 $g: \mathbb{R} \to [0, \infty)$,定义为 $g(x) = x^2$。这里,目标集合是所有非负实数。
- 选取任意 $y \in [0, \infty)$(目标集合 $[0, \infty)$)。
- 构建方程: 设 $g(x) = y$,即 $x^2 = y$。
- 求解 $x$: $x = \pm\sqrt{y}$
- 验证 $x$ 的有效性: 因为我们选取的 $y$ 必须是非负实数($y \ge 0$),所以 $\sqrt{y}$ 总是实数。这意味着 $x = \sqrt{y}$ 和 $x = -\sqrt{y}$ 都是实数。由于原像集合是 $\mathbb{R}$,这两个解都属于原像集合。我们只需要找到至少一个 $x$ 即可。
因此,映射 $g(x) = x^2$ (当目标集合是 $[0, \infty)$ 时)是满射。
例题 3:一个不是满射的例子
考虑映射 $h: \mathbb{R} \to \mathbb{R}$,定义为 $h(x) = x^2$。这里,目标集合是所有实数。
- 选取任意 $y \in \mathbb{R}$(目标集合 $\mathbb{R}$)。
- 构建方程: 设 $h(x) = y$,即 $x^2 = y$。
- 求解 $x$: $x = \pm\sqrt{y}$
- 验证 $x$ 的有效性: 问题来了。如果我选取一个负数,比如 $y = -1$,那么方程就变成了 $x^2 = -1$。在实数范围内,这个方程无解。这意味着对于目标集合 $\mathbb{R}$ 中的负数元素,我们无法在原像集合 $\mathbb{R}$ 中找到对应的 $x$。
因此,映射 $h(x) = x^2$ (当目标集合是 $\mathbb{R}$ 时)不是满射。这个例子清楚地说明了目标集合的定义是多么重要。
为什么满射在函数理论中如此重要?它和值域有什么关系?
满射,或者说“映上”的性质,在函数理论中扮演着核心角色,它关乎映射的“覆盖能力”。对我来说,它就像是确保一个系统没有“死角”或“盲区”的关键属性。如果一个函数是满射的,那就意味着它的输出能力完全匹配了我们所期望的所有可能结果。
满射的重要性体现在几个方面:
- 完整性与覆盖: 满射保证了目标集合中的每一个元素都有其对应的原像。这在很多应用中都至关重要,比如在数据处理中,如果一个转换函数是满射的,意味着所有可能的目标状态都能被原始数据所生成;在密码学中,一个好的加密函数如果能被视为满射,那么每个可能的密文都能由某个明文产生。
- 逆函数的存在条件: 这是一个非常实际的应用。一个函数要拥有一个真正的逆函数,它必须既是单射(一对一)又是满射(映上)。如果不是满射,那么逆函数在目标集合的某些部分就没有定义,因为它找不到对应的原像。
- 抽象代数中的同态与同构: 在群论、环论等抽象代数领域,满射同态(epimorphism)意味着两个代数结构在某种程度上是“等价”的,至少目标结构可以被原像结构完全“生成”或“覆盖”。而满射和单射的结合(同构)则意味着两个结构在代数意义上是完全相同的。
- 资源利用与效率: 从某种角度看,满射也意味着“目标集合”这个空间被充分利用了,没有哪个部分是函数永远无法触及的。
满射与值域的关系:
理解满射与值域的关系,是理解满射概念的关键。 一个映射 $f: A \to B$ 的值域(Range),通常表示为 $Im(f)$ 或 $f(A)$,是原像集合 $A$ 中所有元素通过映射 $f$ 得到的实际输出值的集合。也就是说,$Im(f) = {f(x) \mid x \in A}$。
而一个函数是满射的,当且仅当它的值域等于它的目标集合。用符号表示就是:$f$ 是满射 $\iff Im(f) = B$。
这实际上提供了一种证明满射的替代方法:有时,我们不直接通过解 $f(x)=y$ 来找 $x$,而是先计算出函数的值域,然后比较这个值域是否与给定的目标集合完全一致。
举个例子:
我们再看 $h: \mathbb{R} \to \mathbb{R}$,定义为 $h(x) = x^2$。 它的值域是什么?无论 $x$ 取任何实数,$x^2$ 的结果总是非负的,即 $x^2 \ge 0$。所以,$Im(h) = [0, \infty)$。 而这个映射的目标集合是 $\mathbb{R}$。 显然,$Im(h) = [0, \infty) \neq \mathbb{R}$。因此,$h$ 不是满射。这与我们前面通过找 $y=-1$ 无法找到原像的结论是一致的。
反过来,对于 $g: \mathbb{R} \to [0, \infty)$,定义为 $g(x) = x^2$。 它的值域依然是 $Im(g) = [0, \infty)$。 这次,目标集合也是 $[0, \infty)$。 因为 $Im(g) = [0, \infty)$ 等于目标集合 $[0, \infty)$,所以 $g$ 是满射。
所以,满射和值域的关系非常直接:满射就是值域完全覆盖目标集合的函数。
在实际问题中,我们如何判断一个映射是否可能不是满射?
在实际操作中,判断一个映射是否可能不是满射,往往需要一些直觉、经验和对函数行为的深刻理解。它不是一个机械的过程,更像是一种“侦探工作”,去寻找那些函数“触及不到”的目标元素。
我的经验是,可以从以下几个角度去思考和“嗅探”潜在的非满射情况:
-
观察函数的基本形态和特性:
- 有界函数: 如果函数的值域天生有上下限,比如三角函数 $f(x) = \sin(x)$,它的值域永远在 $[-1, 1]$ 之间。如果它的目标集合是 $\mathbb{R}$,那它肯定不是满射。指数函数 $f(x) = e^x$ 的值域是 $(0, \infty)$,如果目标集合包含负数或零,它就不是满射。
- 偶函数: 像 $f(x) = x^2$ 或 $f(x) = |x|$ 这样的偶函数,它们的输出值通常是非负的(或非正的,取决于具体形式)。如果目标集合包含了正负两部分,那它很可能不是满射。
- 常数函数: $f(x) = c$(一个常数)。它的值域只有一个元素 ${c}$。除非目标集合恰好就是 ${c}$,否则它几乎不可能是满射。
- 分式函数中的渐近线: 比如 $f(x) = \frac{1}{x}$,它的值域是 $\mathbb{R} \setminus {0}$(所有非零实数)。如果目标集合是 $\mathbb{R}$,那么 $0$ 就没有原像,它不是满射。
- 多项式函数的极值: 对于次数为偶数的多项式函数(如二次函数 $ax^2+bx+c$,四次函数等),它们通常会有全局最大值或最小值,这意味着它们的值域会有一个边界。如果目标集合超出了这个边界,那就不是满射。
-
尝试“反向操作”:
- 在脑海中,试着从目标集合中随意取一个元素 $y$,然后尝试解 $f(x) = y$。如果在某个 $y$ 值上,你发现 $x$ 无解,或者解出的 $x$ 不在原像集合 $A$ 中,那么这个函数就不是满射。
- 特别注意那些在求解过程中可能导致数学上不成立的情况(比如开负数平方根,除以零,对负数取对数等)。这些往往是函数“触及不到”目标元素的信号。
-
考虑原像集合和目标集合的“大小”或“密度”:
- 如果原像集合是有限的,而目标集合是无限的,那几乎可以肯定不是满射。例如,从 ${1, 2, 3}$ 到 $\mathbb{N}$(自然数集)的任何映射都不会是满射。
- 如果原像集合是离散的(如整数集),而目标集合是连续的(如实数集),那么映射也通常不是满射。例如,从 $\mathbb{Z} \to \mathbb{R}$ 的 $f(x) = x$ 就不是满射,因为它只能生成整数,无法生成所有的实数。
-
图示法:
- 如果函数可以被绘制出来,观察它的图像是否“覆盖”了整个目标集合的y轴范围。如果图像在y轴上存在“空隙”或者没有延伸到y轴的某个部分,那么它就不是满射。
总而言之,判断非满射,就是去寻找那些目标集合中“孤独”的元素,它们没有对应的原像。这需要我们深入理解函数的定义域、值域、以及它在不同输入下的行为模式。
除了满射,还有哪些重要的映射性质?它们如何相互关联?
除了满射(Surjectivity),函数还有另外两个同样重要的性质:单射和双射。这三个性质构成了我们理解函数“行为模式”的核心框架,它们就像是描述函数“精准度”和“覆盖度”的不同维度。它们相互关联,共同定义了函数在不同情境下的能力。
- **单射(Inject






























